The plate is subjected to the two forces at A and B as shown.If \theta =60^0,determine the magnitude of the resultant of these two forces and its direction measured clockwise from the horizontal.

Solution:
Let us draw the vector components as follows:

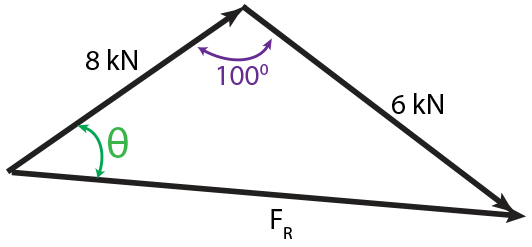
Now, let us draw the vectors tail to tail as follows:

(F_R)^2=8^2+6^2-2(8)(6)\cos100^0
F-R=\sqrt{8^2+6^2-2(8)(6)\cos100^0}
F_R=10.80 kN
Now, we can calculate \theta by using law of sines. (Forgot the Law of Sines?)
\frac{\sin \theta}{6}=\frac{\sin 100^0}{10.80}
\sin \theta = 0.5470
\theta = 33.16^0
Now, to calculate \phi we simply subtract 30^0 from \theta
\phi=33.16^0-30^0
\phi=3.16^0
This question can be found in Engineering Mechanics: Statics (SI edition), 13th edition, chapter 2, question 2-15.



This is really so amazing, wonderful and helpful. keep doing more. thanks
You are very welcome, glad it helped you out! 🙂
How did you get the angles 100 & 80? I can’t figure it out..
You have to use the law of sines to calculate the angles.
is this use parrallelogram method?
The tail to tail method.